-
Kati három dobókockával játszott:
kékkel, pirossal és zölddel. Hány különféle módon dobhatott összesen
5 pontot?
-
Melyik napra esik 1984 január
1.-e?
-
Csupaháj olyan nehéz volt
mint két Nyakigláb, három Nyakigláb annyit nyomott mint 5 Málészáj.
Nyakigláb 50 kg volt. A három barát együtt 10-szer könnyebb egy gépkocsinál.
Milyen nehéz a gépkocsi?
-
Gondolok egy számot. Ha hozzáadok
3-at, majd osztom 10-zel, a legkisebb háromjegyű számot kapom.
Milyen számra gondoltam?
-
Találd meg az összes X törzsszámot,
melyre érvényesek a következő egyenlőtlenségek:
X + 7 > 10
és a 2 . X - 4
< 20
-
Rajzolj tetszés szerinti háromszöget
és oldalainak középpontjait kösd össze szakaszokkal. Hány háromszög
van az ábrádon?
-
Egy doboz méretei: 20 cm, 30
cm és 50 cm. Minden méretét 10%-kal kisebbítjük. Hány százalékkal
kisebbedik a térfogata?
-
A sportversenyen 7 pionír
vett részt. Hány mérkőzést játszottak, ha minden pionír játszott
egymással, de egy a pionírok közül két mérkőzés után
megbetegedett és tovább nem játszott ?
-
Határozzátok meg azt a számot,
amely 5-ször nagyobb mint az 1234 és 4321 számok összege!
-
A kérdőjeleket
helyettesítsétek számokkal úgy, hogy érvényes legyen:
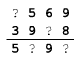
-
A 20-as számot bontsátok
fel három különböző törzsszám összegére.
-
Határozzátok meg az a számot,
amely a 43. helyen lesz ebben a számsorban:
0, 0, 1, 0, 1, 2, 0,
1, 2, 3, ...
-
Hány külömböző pozitív
számot kaptok, ha felírjátok az 1, 2, 3, ... , 100 számok összes
lehetséges különbségét?
-
Írjátok fel a legnagyobb háromjegyű
számot, mely számjegyeinek szorzata 12.
-
Határozzátok meg a két ötödét
annak a legkisebb ötjegyű számnak, melyben nem fordul elő
az 1-es szám.
