Mekkora szöget ír le 35 perc alatt az óra kismutatója?

Melyik számmal kell elosztani a 16-ot, hogy 32-öt kapjunk eredményül?

Számítsátok ki:
437 : 19 - 399 : 19 + 152 : 19 =

Gondoltam egy számra. Ha megszorzom kettővel, elosztom kettővel, megszorzom hárommal, elosztom hárommal, hozzáadok 50-et, kivonok 50-et, akkor 2008-at kapok eredményül. Melyik számra gondoltam?

Hány különböző prímszám van a 180 prímtényezős felbontásában?

Számítsátok ki a háromszögben a belső szögek nagyságainak az összegét, ha a külső szögeinek nagysága: 80° 5', 129° 25', 150° 30'.

A dobozban labdák vannak, amelyeken a 390; 698; 1410; 597; 1000; 50 számok vannak. Írjátok le azoknak a számoknak az összegét, amelyek oszthatóak 15-tel!

Írjátok le milyen számjegy van a tízezredek helyén a szorzatban:
0,006 . 0,005 . 0,03 . 0,2 =

Számítsátok ki:
–1 + { – 1 – [ – 1 – ( – 1 – l ) ] – l } – 1 =

Attila úrnak 0,25 km oldalhosszúságú négyzet alakú kertje van. Ki szeretné cserélni István úr 7 ha területű háromszög alakú kertjével. Hány koronát kell hozzáfizetnie, ha megegyeztek, hogy minden négyzetméterért, amennyivel nagyobbra cseréli, 10 Sk-t hozzáfizet?

Hány egész szám van a számegyenesen a  –10,235  és  10,235  számok között?

Írjátok le a legkisebb eredményt jelző betűt:
A = 0,02 . 0,3 . 0,4
B = (0,2 - 0,3). (0,4 - 0,5)
C = 3,4. (0,05 - 0,0500) . 3,58

Zsófika egy 100-jegyű számot írt le a következőképpen: 100100100100.... Mennyi ennek a számnak a számjegyeinek az összege?

A 6.B osztályba járó tizenegy lány átlagmagassága 158 cm. A 6.B osztályba új diáklány jött, akinek a magassága 160,5 cm. Írjátok le mekkora lett így az osztályban a lányok átlagmagassága! (egy tizedesjegy pontossággal)

A 15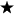0 számban helyettesítsétek be a hiányzó számjegyet úgy, hogy a kapott szám 12-vel osztható legyen. Írjátok le az összes ilyen számjegyet!