-
Számítsd ki
az összes olyan egész szám összegét, amely kielégíti az
egyenlőtlenséget:
– 26 ≤ x ≤
30
-
A gyümölccsel teli láda hétszer nehezebb az üres
ládánál. Gyümölccsel tele 30 kg-mal több a tömege, mint üresen.
Határozd meg az üres láda tömegét!
-
Helyettesítsd be a következő három
számot a sorozatba és írd le az összegüket:
10, 1, 11, 11, 12, 111, 13, ..., ..., ...
-
Írd le melyik szám van a számegyenesen
pontosan a 14,8 és a –12,4
között?
-
Melyik az a szám, amelyiket ha
megszorozzuk héttel ugyanazt az eredményt adja, mintha kivonnánk
belőle 60-at?
-
Számítsd ki:
( 25 365
– 2 567 ) + ( 35 167 – 5 365 ) + ( 34 678 –
5 167 ) + ( 12 567 – 4 678 ) =
-
Az egyenlő szárú háromszögnek az alapja 10 cm
hosszú. Az alappal szemben fekvő szög
nagysága egyenlő az alapon fekvő szögek nagyságának az összegével.
Számítsd ki a háromszög területét!
-
Milyen törzsalakú törttel kell
megszoroznunk a
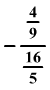 törtet, hogy a szorzat 1 legyen?
törtet, hogy a szorzat 1 legyen?
-
Húzz ki a 987 654 321
számból két számjegyet úgy, hogy a lehető legnagyobb tizenkettővel
osztható számot kapd! Írd le ezt a számot!
-
Milyen törzsalakú törtet kell a
* helyére írni:
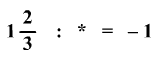
-
Milyen számmal kell a 12 345 679-et
megszorozni, hogy az eredmény 444 444 444 legyen?
-
Az anya most 37, a lánya 9 éves. Hány
éves volt a lánya akkor, amikor az anya ötször olyan idős volt, mint
a lánya?
-
A könyv oldalainak megszámozására 159 számjegyet
használtunk fel. A számozást így kezdtük: 1, 2, ... . Hány
oldalas a könyv?
-
Hányszorosára növekszik a 6,72 dm élű kocka
térfogata, ha minden élét háromszorosára növeljük?
-
Írd le a hattal való osztás utáni
lehetséges maradékok összegét!
