-
Írd le azt a betűt, amelyik
a legkisebb számot jelöli:
A) 0,5 . 1,5 . 2,5
B) 0,05 . 1,5 . 2,5
C) 0,005 . 1,5 . 2,5
-
A számegyenesen ki vannak
jelölve a 3,2 és 7,8 számok.
Számítsd ki azoknak a számoknak az összegét, amelyek ugyanolyan messze
vannak a 7,8-tól, mint az 5 a
3,2-től.
-
A trapézban a szögek aránya
3:4:5:6. Számítsd ki a trapéz belső szögei összegének a felét!
-
Milyen számjegyekkel
helyettesíthetjük a *-ot a 72*00000000133
számban, hogy osztható legyen 3-mal? Számítsátok ki a szorzatukat!
-
Számítsd ki és az eredményt
írd le törzsalakban:
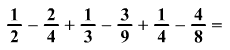
-
Számítsd ki:
5 . (–5) . 0,5 . (–0,5) . 2 . (–2) . 0,2 . 0,2 =
-
Az ötszázjegyű
12381238... számban az 1, 2, 3, 8 számjegyek periodikusan
váltják egymást. Hányszor írjuk le a 8-as számjegyet?
-
Bontsd fel a 2310-et
prímtényezők szorzatára és írd le azt a prímszámot, amely közülük a
legnagyobb!
-
Milyen számjegyre végződik
a 78354 és a 40011 számok
szorzata?
-
Az edénynek a kofolával
együtt 21 kg a tömege. Ha csak félig van ez edény töltve
kofolával, akkor 11 kg a tömege. Mekkora az edény tömege?
-
Hány részre osztja fel az
ábrán az olimpiai ötkarika az olimpiai zászlót?
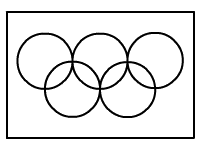
-
Pista felírt egy
tetszőleges hatjegyű számot, majd hozzáadott egymilliót. Hányjegyű
számot kapott eredményül?
-
Hányszor írod le a
9-es számjegyet a 100 000 000 és az 1
különbségének eredményében?
-
Van Szlovákiában hat város,
amely autóbuszközlekedéssel van összekötve. Hány különböző autóbuszjárat
ez, ha Pozsonyból a járat Nagyszombatba ugyanaz, mint vissza?
-
Számítsd ki:
– 11,5 – 11,4 – 11,3 – 11,2 – 11,1 + 20,5 + 20,4 + 20,3 + 20,2 + 20,1 =
