-
Milyen számot takar a
maszat az egyenlőségben?
 .
(–2,3) = 7,038
.
(–2,3) = 7,038
-
Oldd meg az egyenletet és
írd le azt a számot, amely kielégíti:
3x + 5,7 = 2x – 3,1
-
Melyik az a negatív szám,
amely a számegyenesen a 34-től háromszor olyan messze van, mint a
–2-től?
-
Ferkó összeszorozta az
összes egész számot –8-tól 9-ig. Írd le a
szorzásának helyes eredményét!
-
Gyuri egy zacskó cukorkát
kapott. Barátaival először megette a cukorkáinak a felét, majd a
zacskóból két szemet Lilinek adott. Utána otthon a testvéreivel megette
annak a harmadát, ami a zacskóban maradt és kettőt még az anyukájának
adott. A megmaradt 4 szem cukorkát elrakta. Hány szem cukorkát kapott
Gyuri?
-
Számítsd ki az A, B, C
számok összegét, ha érvényes:
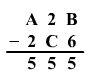
-
Számítsd ki annak a
téglatestnek a felszínét, amelynek egy 36 cm2 területű
négyzet az alapja és a magassága l dm. Az eredményt
négyzetdeciméterekben írd le!
-
Számítsd ki:
68 . 23 + 70 . 23 + 72 . 23 – 69 . 23 – 71 . 23
-
Számítsd ki a 434
tizenhárom hetedét!
-
A legnagyobb hattal
osztható 5-jegyű számból vond ki a legkisebb kilenccel osztható 4-jegyű
számot!
-
A 432 897 561 számból
húzz ki 2 számjegyet úgy, hogy a lehető legkisebb 6-tal osztható számot
kapd! Írd le az így kapott számot!
-
Családunk életkorának
számtani középértéke 23,5 év. Anyuka 36 éves, apuka 2 évvel idősebb. Én
12 éves vagyok. Hány éves családunk utolsó tagja, a húgom?
-
Írd le a feladat eredményét:
6 006 : 24 . 4 =
-
Gyurinak kilenc liter vizet
kell elhoznia háromnegyed literes üvegekben. Hány üveget kell hoznia?
-
Hány különböző féle képpen
írhatjuk fel a 30-at három különböző természetes szám szorzataként (a
tényezők sorrendje nem számít)?
