A  2 cm  és  5 cm  oldalú téglalapot olyan négyzet alakú részekre akarjuk osztani, amelyeknek az oldala egész szám. Legkevesebb hány részt kaphatunk?

Mi a több:   10 . 10 . 10 . 10 . 10 : 2 : 2 : 2 : 2 : 2   vagy   5 . 5 . 5 . 5   ?

Rajzoljatok egy olyan hatszöget, melynek öt belső szöge derékszög!

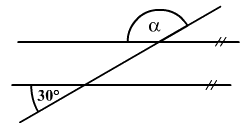
Számítsátok ki az ábrán látható  α  szöget.

Számítsátok ki az alábbi számok számtani középértékét (aritmetikai átlagát):
10,5   ;      10,6   ;      10,7   ;      10,8   ;      10,9

Hány cm²-rel nagyobb a  2,5 dm  élű kocka felszíne, mint a  250 mm  élű kocka felszíne?

Számítsátok ki:   – 4 + ( – 3 ) – ( – 5 ) – ( + 6 ) – ( – 7 )

Milyen számjegyre végződik a következő szorzat:   22 . 54 . 18   ?

A síkban adottak a  B, R, U, M  pontok. Állapítsátok meg a RUB nem konvex szög lehető legnagyobb értékét, ha tudjátok hogy az RUM szög nagysága 30° és a BUM szög nagysága 40°.

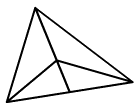
Hány háromszög van az alábbi ábrán?

Hányszor használjuk a 3-as számjegyet, ha 1-től 100-ig leírjuk az összes számot?

Mennyi a héttel való osztás során lehetséges összes maradék összege?

Az  1734,  1743,  3417,  3471  és  7134  számok közül melyik számok oszthatók maradék nélkül 17-tel?

A  12 cm  kerületű rombuszt két egyenlő oldalú háromszögre vágtunk szét. Mekkora a kerülete az egyik háromszögnek?

A következő helyesen kiszámolt példába írjátok be a hiányzó bal zárójelet:
2 . ( 11 + 3 . 7 – 2 . 2 ) )  =  40