-
Számítsd ki az ábrán látható
α szög nagyságát!

-
Melyik az a szám a –29,
–8, 5, 2 és a 14 számok közül,
mely egyenlő a többi négy összegével?
-
Pótold a hiányzó zárójelet
úgy, hogy az összeg a lehető legnagyobb legyen:
– ( 13 + 11 – 9 + 7 – 5 + 3 – 1
-
Írd le a 25763 :
0,0001 szám középső számjegyét.
-
A számkártyákból az ábrán
látható alakzatot raktuk ki úgy, hogy a sorban és az oszlopban levő
számok összege –1. Melyik szám van középen?

-
Hány kis négyzetet
tartalmaz a fekete négyzet, melynek csúcsai a négyzetháló rácspontjaiban
vannak. A négyzet egy részét az alábbi ábrán látjátok.

-
Van három téglalapunk,
melyekből kirakható egy négyzet (a téglalapok nem fedik egymást).
A téglalapok hosszabbik oldalai 4 cm, 5 cm
és 6 cm hosszúak. Mekkora a téglalapokból
kirakott négyzet területe?
-
Melyik az alábbi szorzatok közül
a legnagyobb?
2,3 . 8 ; 3,4 . 7
; 4,5 . 6
; 5,6 . 5
; 6,7 . 4
-
Mekkora az egyenlő szárú háromszög
kerülete, ha két oldala 2 cm és 5 cm hosszú?
-
Milyen szám van a számegyenesen
a –0,7 és az 1,4 számok között középen?
-
A VI.B osztályban nincs két
egyforma magas lány. Hét lány magasabb Jankánál, három pedig
alacsonyabb. Hány lány van a VI.B osztályban?
-
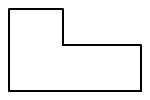
Hány derékszöget látsz az
alábbi ábrán?
-
Számítsd ki az
546, 18 és 66 legnagyobb közös osztóját!
-
Mekkora a kocka térfogata,
ha felszíne 294 cm2?
-
Számítsd ki: 4
– { 1,6 – [ 1,2 – ( 1,5 – 2 ) ] } =
