-
Az ismeretlen szám felének
négyszerese 123-mal kisebb mint az ismeretlen szám. Határozd meg
ezt az ismeretlen számot.
-
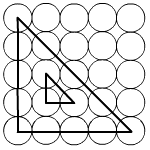
Az ábrán látható kisebb háromszög
területe 2 cm2. Mekkora a nagyobb háromszög területe?
-
Milyen számot takar a
tintafolt az egyenlőségben?
 : 4 = 10 : 7
: 4 = 10 : 7
-
Számítsd ki:
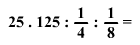
-
Majka, Béla és Janka együttesen
32 gesztenyét találtak. Ha Majka még 4 gesztenyét talált volna,
akkor 2-vel több gesztenyéje lenne mint Bélának és 2-vel kevesebb
mint Jankának. Hány gesztenyét talált Janka?
-
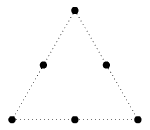
Az ábrán kijelölt pontokból
hány háromszög szerkeszthető úgy, hogy csúcsaik a kijelölt
pontokban vannak?
-
A –61,73 szám
számjegyei közé helyezd el az 5-ös számjegyet úgy,
hogy 0,157-tel nagyobb szám keletkezzen.
-
A téglatest méretei egész
számokra kerekítve 5 cm, 6 cm és 7 cm. Határozd meg
a hasáb lehető legkisebb egészszámú térfogatát.
-
Mekkora az 1000 liter térfogatú
kocka felszíne?
-
Melyik szám az
a), b), és c) példákban a legkisebb:

-
Hány literrel kevesebb
az 5/2 hl mint a 7/25 m3?
-
Milyen számjeggyel pótolható
a k úgy, hogy a 4k1k2k3 szám osztható
legyen 3-mal?
-
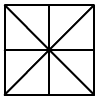
Hány ötszög van az ábrán?
-
Kofola pohárral együtt
12,60 Sk-ba kerül. A kofola 12 Sk-val drágább a pohárnál.
Hány koronába kerül a kofola?
-
Golyókat osztunk szét 7,
majd 8, majd 6 gyerek között úgy, hogy a gyerekeknek minden leosztásban
egyforma számú golyójuk van. Legkevesebb hány golyóra van szükségünk,
hogy elvégezhessük ezt a leosztást?
