A  18,  36,  56,  78  és a  216  számok között van egy szám, mely nem rendelkezik azzal az oszthatóság szempontjából közös tulajdonsággal, amellyel a többi szám rendelkezik. Melyik ez a szám?

A  –2,  +3,  –5,  +6,  –1,  –4,  +1  számok közül írjátok le azokat a számpárokat, melyek összege egyenlő –1-gyel.

Sorold fel az összes olyan negatív egész számot, amely nagyobb az alábbi különbségnél:
– 8,36 – ( + 1,64 )

Milyen számjegy lesz a tizedek helyén a  0,0063  és a  0,603  számok szorzatában?

Határozzátok meg azoknak a számjegyeknek az összegét, amelyekkel pótolhatjuk a csillagot a  30432  számban úgy, hogy ez a szám osztható legyen 4-gyel.

A koromat, vagyis az éveim számát leírhatom olyan számmal, mely a 242-nek a legnagyobb kétjegyű osztója. Hány éves vagyok?

A TRAVOLTA tánckörben annyi fiú és lány van, hogy táncolhatnak hármasával, négyesével, de nyolcasával is. Hány lehető legkevesebb tagja van a tánckörnek?

Mit írhatunk a kör helyébe a következő algebrai kifejezésben, hogy érvényes legyen az egyenlőség?
– ( 3x³ + O – 5x² – 4 ) = – 2x³ + 6 – 3x² + x – x³ + 8x² – 2

Számítsátok ki az ábrán látható satírozott rész területét, ha tudjátok, hogy a kerülete 25,2 cm. Megjegyzés: az alakzat négyzetekből van kialakítva.

Hányad része van besatírozva az ábrán látható téglalapnak? Fejezzétek ki törttel és tizedes számmal is.

Mennyivel nagyobb a  8/9  tört a  6/7  törtnél?

Számítsátok ki az ábrán látható ABCD trapéz DAB szögének nagyságát.

Az alábbi törtek közül válaszd ki azokat a párokat, amelyek összege 1.

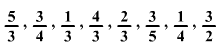
Öcsém és én a lakás szombati takarítását 1 óra 15 perc alatt végezzük el. Ha csatlakozik hozzánk a húgunk, és ugyanolyan gyorsan dolgozik mint mi, akkor még egy kirándulásra is elmehetünk. Hány órakor mehetünk el kirándulni, ha pontosan 7:00 órakor kezdtünk takarítani?

Milyen arányban osztozkodott három barát az évközben gyűjtött 450 telefonkártyán, ha az első kétszer annyit kapott mint a második, a harmadik pedig három ötödét annak, amit a második?