Mivel egyenlő azon számjegyek összege, amelyeket a csillagok helyébe írhatunk úgy, hogy az egyenlőség érvényes legyen?
( 444 ) : 124  =  ( 16 : 36 ) . ( 88 : 48 )

Milyen számot kapunk, ha összeadunk 11 százast, 5 tízest, 16 egyest, 5 tizedet és 16 századot?

Milyen egész számot írhatunk a körbe úgy, hogy érvényes legyen az egyenlőtlenség:
21,21  <  10,61 . O  <  21,23

Valentin mondja Rózsikának: háromszor annyi idős vagyok, mint amennyi te voltál akkor, amikor én voltam annyi idős, mint te most. Ha annyi idős leszel mint én most, akkor együtt 112 évesek leszünk. Hány éves Rózsika?

Három egymás után következő páratlan természetes szám összege 27. Melyik közülük a legnagyobb?

Egy iskola tanulóinak létszáma nagyobb mint 500, de kisebb mint 1000. Ha a tanulókat szétosztanánk osztályokba 18-asával vagy 20-asával vagy 24-esével, mindig kimaradna 9 tanuló. Hány tanuló van az iskolában?

Határozd meg azon hárommal osztható háromjegyű számok összegét, melyeket a 2, 3, 4-es számjegyek felhasználásával alkothatunk. A számjegyek a számban nem ismétlődhetnek.

Hány hét a  2 419 200  másodperc?

A  6.c osztály öltözőjében 54 cipő és 11 sapka van. Hány tanuló jött az iskolába sapka nélkül?

Milyen számot írhatsz az ismeretlen Y helyébe a körbe?

A fiúk megegyeztek, hogy közösen vesznek egy futball-labdát. Ha mindegyikük 6 koronát adna, akkor még 16 korona hiányozna. Ha viszont mindegyikük 7 koronát adna, akkor 4 koronájuk megmarad. Hány fiú volt a csapatban?

Az  E, F;  G, H;  I, J;  K, L  pontokkal a 9 cm oldalhosszúságú ABCD négyzet minden oldalát három egyenlő részre osztottuk (lásd az ábrát). Számítsd ki az EFGHIJKL alakzat területét.

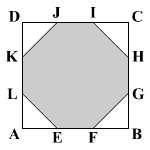
Számítsd ki az ábrán besatírozott rész kerületét, ha tudjátok, hogy területe 36 cm². Megjegyzés: az alakzat négyzetekből van kialakítva.

Egy almával telerakott kosár tömege 34 kg. Ha a kosarat félig rakjuk almával, akkor a tömege 17,5 kg. Mekkora a kosár tömege?

A  3,1 cm élhosszúságú kocka egyik oldallapjának közepébe egy 1 cm élhosszú négyzet keresztmetszetű nyilást vágunk. Mekkora a keletkezett test térfogata?