-
Mojmírnak 3-szor több bélyege
van, mint Svätopluknak, de 3-szor kevesebb mint Rastislavnak. Összesen
169 bélyegük van. Hány bélyege van Mojmírnak?
-
Pótold a sorozat következő
3 tagját.
3 , 5 , 7 , 11 , 13 , 17 , 19
, 23 , 29 , ...
-
Számítsd ki:
0,0084 : 0,35 =
-
Egy 144 cm3 köbtartalmú
hasáb alapját 6 darab 15 cm2 területű háromszögre
osztottuk. Számítsátok ki a hasáb magasságát!
-
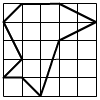
Hány sokszöget látsz az ábrán?
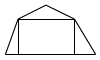
-
A
 ,23
. 1,
,23
. 1, 7 = 1
- 0,661
7 = 1
- 0,661 egyenlőségben
pótold a csillagokat megfelelő számjegyekkel.
egyenlőségben
pótold a csillagokat megfelelő számjegyekkel.
-
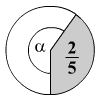
A képen a 2/5
tört van ábrázolva. Számítsátok ki az α
szög nagyságát.
-
Milyen számjegyeket írhatunk
a csillag helyébe, hogy a 35 79432
szám osztható legyen 6-tal?
79432
szám osztható legyen 6-tal?
-
Számítsátok ki az ábrán
látható sokszög területét, ha a kis négyzetek oldala 10 mm nagyságú.
-
Hány háromjegyű prímszám
végződik 5-re?
-
Határozd meg, hogy mennyivel
kisebb vagy nagyobb a
- 34 768
a - 43 105 -nél.
-
Legfeljebb hány 37,5 cm
hosszú és 5,6 cm széles lecet lehet kivágni 3 darab 217 cm hosszú
és 12,2 cm széles deszkából?
-
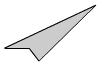
Határozd meg az ábrán látható
négyszög belső szögeinek összegét.
-
Gondoltam egy számot. Ha
megszorzom 9-cel, az eredményből kivonok 20-at, és ezt az eredményt
elosztom a gondolt számmal, a gondolt számot kapom. Legalább egy számot
találj, amelyre gondoltam!
-
Péter leírt egy törtet,
melynek nevezője 84. Péter által leírt tört egyenlő
az 5/12 törttel. Mennyi a Péter által leírt tört
számlálója?
