A   367 + 258 = 625   összeg mindegyik számában húzzatok át egy számjegyet úgy, hogy érvényes legyen az egyenlőség.

Hány négyzet alakú csempére van szükségünk  10 cm  hosszú oldallal egy  3,6 m  hosszú és  2,5 m  széles folyosóra?

Számítsátok ki:
a.)   ( 19,1 . 2,1  +  7,7  +  2,1 . 0,9 ) : 0,71
b.)   1,023  +  0,1007  +  2,9999  +  3,73

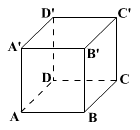
A képen adva van egy kocka az  A, B, C, D, A', B', C', D'  csúcsokkal. Hány külömböző egymással párhuzamos egyenes van az adott kockában?  (Minden egyenes az  { A, B, C, D, A', B', C', D' }  halmaz pontjaival van meghatározva.)

Számítsátok ki:    1987 . 1988  .

A tornán 5 csapat játszott "mindenki mindenkivel" módon. Egy csapat két mérkőzés után kilépett a versenyből. Hány mérkőzést játszottak le összesen?

Egy tégla 4 kg-ot nyom. Milyen nehéz a tégla három negyedének az egy harmada?

Milyen lesz a maradék, ha az   1 + 2 + 3 + ... + 30   számot elosztjuk 3-mal?

Adva van egy téglatest  10 cm-es,  6 cm-es és  5 cm-es élekkel. Hányszor kisebbedik a téglatest felszíne, ha minden élét a felére rövidítjük?

Az ismeretlen szám nyolcszorosa egyenlő a 32 háromszorosával. Melyik az a szám?

Fejezzétek ki a 18-at mint három törzsszám összegét!

Három szám összege 77.  A legnagyobb közülük a legkisebb háromszorosa, a középső a legnagyobbik fele. Határozzátok meg az összeadandókat!

Hány különböző módon állhatnak sorba Éva, Marika, Jóska és Tamás úgy, hogy az első fiú és az utolsó lány legyen?

Számítsátok ki:    - 1236 - [ - 134 - ( - 232 ) + 320 ]  .

Keressétek meg a 210 és a 60 számok minden közös osztóját.