Írjátok fel az egyes számot 5 hetes és a számtani műveletjelek segítségével.

Hány kilogramm széna fér bele  9,4 m hosszú,  5 m széles szénatartóba, ha a szénát  3,5 m magasra rakhatjuk, és ha  1 m³ friss széna súlya  82 kg.

Írjuk fel azt a legkisebb négyjegyű számot, amely 3-mal és 7-tel osztható.

Az  A, B, C betűket helyettesítsétek számokkal úgy, hogy érvényes legyen:
AA  +  BB  =  CC0

A nyári szünidő az év  1/6 része, a téli  1/30 része, a tavaszi az év  1/45 része, a szombatok és vasárnapok egy tanévben az év  2/9 részét teszik ki. Az év hányad részét teszik ki a szabad napok és hányad a tanítási napok?

Az  X-et helyettesítsétek úgy, hogy a  14 X21 osztható legyen 49-cel!

Három szám szorzata  39 900. Az egyik szorzótényező  14 a másik  38. Keressétek meg a harmadik tényezőt!

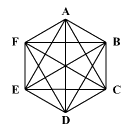
Hány különböző négyszög látható a képen? (A négyszög csúcsai az {A, B, C, D, E, F} halmazból valók.)

Melyik szám következik ezek után a számok után?
2,  7,  22,  67,  ...

Keressétek meg azt a legnagyobb négyjegyű számot, amely számjegyeinek összege 33 !

Az üzemben  1256 munkás dolgozik. Ebből  615 férfi. Fejezzétek ki százalékban a nő dolgozók számát!

Írjátok fel a legkisebbtől a legnagyobbig:

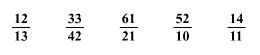
Három egymás után következő szám összege 2370. Melyek ezek a számok?

Milyen napra esett 1982 június 1.? (Ha 1982 január 1. péntek volt.)

Egy kétszáz oldalas könyvben hányszor található meg az ötös számjegy, ha minden oldal meg van számozva?