Számítsd ki:
1375  -  485  +  85  =

Milyen számjeggyel végződik a példa eredménye?
27 . 53  -  13 . 5  =

Két összeadandó összege 63. Ez az összeg 37-tel nagyobb, mint az első összeadandó. Számítsd ki a másik összeadandót.

Hány megoldása van az egyenlőtlenségnek?
17  <  x + x  <  50

Oldd meg az egyenletet:
x  +  x  +  x  =  32  +  x

Az 543, 545, 547 és 549 számok közül melyik az a szám, mely 7-tel osztva a legkisebb maradékot adja?

Határozd meg a számsorozat következő három számát:
51 , 49 , 48 , 46 , 45 , 43 , 42 , ...

Számítsd ki:
2002 : 14 . 7

Írd be a hiányzó műveletjeleket úgy, hogy az egyenlőség érvényes legyen:
6       2       3       4  =  13

Az A városból a B városba három út vezet. A C városból a B városba négy út vezet. Hányféle módon juthatunk el az A városból a C városba, ha egyik út sem keresztezi egymást?

Melyik két kétjegyű szám szorzata 1025 ?

Hány kétjegyű szám számjegyeinek összege 5 ?

Írj valamennyi csillag helyére egy-egy számot úgy, hogy érvényes legyen az egyenlőség:
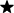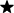
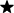2  .  6   +   9   =   1

Öt poharat és három tányért vettünk. Ugyanannyit fizettünk az 5 pohárért, mint a 3 tányérért. Összesen 120 koronát fizettünk. Hány koronába kerül egy pohár?

Janika 9 évvel idősebb Misinél. Misi 3 évvel fiatalabb Petinél. Hány évvel lesz idősebb Janika Pétertől 4 év múlva?