Egy kétszámjegyű számot exkluzívnek nevezünk akkor és csak akkor, ha a számjegyei szorzatához hozzáadva a számjegyei összegét az eredeti számot kapjuk. Például 79 exkluzív szám, mert 79 = 7 · 9 + (7 + 9) . Találjátok meg az összes exkluzív számot.

A  cm oldalhosszúságú szabályos hatszög belsejében egy  1 cm hosszúságú átmérővel kör mozog úgy, hogy állandóan érinti a szabályos hatszög kerületét. Számítsátok ki a területét a hatszög azon részének, amelyet az így mozgó kör soha se nem fed le.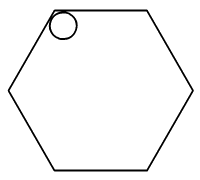

Hányféleképpen lehet az {1, 2, ... , 8, 9} számhalmazból kiválasztani hét számot úgy, hogy azok összege osztható legyen hárommal?

Adva van egy egyenlő területű kör és négyzet. Az adott körbe írjunk be négyzetet és az adott  négyzetbe kört. Melyik beírt geometriai alakzat területe nagyobb?

Páros úrnak páros számú juhocskája, Páratlan úrnak páratlan számú juhocskája volt. Összesen e két úr juhocskáinak a száma egyenlő számokból álló háromszámjegyű szám. Páros úr mindegyik juhocskája három juhocskát, Páratlan úr mindegyik juhocskája két juhocskát elett. Egyik nap Páros úrnak három juhocskáját széttépte a farkas. Így most Páros és Páratlan úr juhocskáinak a száma egyenlő. Hány juhocskája volt eredetileg mindegyik tenyésztőnek?

Öt gyermek egymás után a következőt mondta:
   ”Tegnap hétfő volt.”
   ”Ma csütörtök van.”
   ”Holnapután péntek lesz.”
   ”Holnap szombat lesz.”
   ”Tegnapelőtt kedd volt.”
Ha tudnátok, hogy hány gyermek hazudott, akkor rögtön világos lenne, hogy milyen nap van ma. Milyen nap van ma?