Ha két téglalap összebarátkozik, oldalaik egymáshoz simulnak úgy, hogy legalább egy közös csúcsuk legyen.

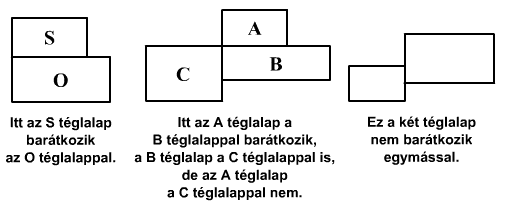
Nemrég összebarátkozott három téglalap, mindegyik mindegyikkel. Az első méretei 3 cm x 7 cm, a másodiké 5 cm x 8 cm, a harmadiké 2 cm x 8 cm. Barátkozásukkal létrehoztak egy alakzatot, amelynek kerülete a lehető legnagyobb. Mekkora ez a kerület?

A fenti tíz kártyából kiválasztottunk hatot úgy, hogy belőlük két olyan háromjegyű számot képezhessünk, amelyekre egyidejűleg érvényes:

• egyikük maradék nélkül osztható 9-cel,

• összegük olyan szám, amelynek csak páratlan számjegyei vannak.

Keresd meg azt a két háromjegyű számot, amelyek megfelelnek mindkét feltételnek és ráadásul összegük a lehető legnagyobb!

Zsuzsi tarisznyájában 15 piros, 3 zöld és 8 kék golyó van. Minden egyes benyúlással kivesz a tarisznyából 2 golyót, amelyeket nem néz meg, és nem tesz vissza. Legalább hányszor kell a tarisznyába nyúlnia ahhoz, hogy a kivett golyók között biztosan legyen legalább egy zöld? Legalább hányszor kell a tarisznyába nyúlnia ahhoz, hogy legalább egyszer két piros golyót húzzon ki egyszerre?

Misi az első ábrán látható téglalapot néhány háromszögre nyírta szét. Az így nyert háromszögek mindegyikének felhasználásával össze tudja rakni a második ábrán látható háromszöget is, és a harmadik ábrán látható paralelogrammát is.

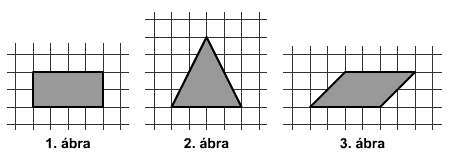
Állapítsd meg, hogyan osztotta fel Misi a téglalapot, ha a háromszögek száma
    a)    4
    b)    3 volt!
Az  a),  b)  esetek mindegyikéhez húzd meg a vonalakat, amelyek mentén Misi nyírhatott! Továbbá rajzold le a második és a harmadik ábra alakzatait is úgy, ahogy a kis háromszögekből összerakhatók. Az összeillesztésnél a háromszögek nem fedhetik egymást és az alakzat nem lehet hézagos.

Virág és Gabika hörcsögöt tartanak. Tegnap Virágnak tízzel több hörcsöge volt, mint Gabikának. Az éjszaka folyamán Virágnál és Gabikánál is 5 hörcsög jött világra, így most Virág hörcsögeinek száma kétszer annyi, mint Gabika hörcsögeié. Hány hörcsöge van Virágnak, és hány Gabikának?

A furfangos Matyi nagyon szereti a matematikát. Tegnap felfedezett egy hosszú, 2004 darab lécből álló kerítést. A kerítésre krétával többször ismételten ráírta a MATEMATIKA szót. Minden lécre, az elsőtől az utolsóig, csak egy betűt írt: először az M-et, azután az A, T, E, M, A, T, I, K, A, M, A, T, E stb. betűket. Milyen betű került az utolsó lécre? Hányszor írta le az M betűt?