Vegyünk egy különböző számjegyekből álló négyjegyű számot. Minden számjegyét helyettesítsük a fennmaradó számjegyek számtani közepével. Melyik lesz az így keletkező legkisebb, ill. legnagyobb szám?
A konvex négyszög átlója felezi a szemközti oldalak felezőpontjait összekötő szakaszt. Bizonyítsátok be, hogy az átló a négyszög területét is felezi.
Oldjátok meg a következő
egyenletrendszert:
x + y10 = 98,7
x10 - y = 23,4
ahol y10 a tízesekre kerekített y szám és x10
a tízesekre kerekített x szám.
Három jóbarát egy kör alakú tóban fürdött. Mindhárman ugyanarról a helyről és egy időben ugrottak a vízbe. Juli egyenesen délnek úszott, Vera keletnek és Sztano egyenesen a tó középpontján át. Mindenki ugyanabban az időpillanatban ért partot, és megállapították, hogy ha Veránál találkoznának, akkor a part mentén együttesen negyedrészével hosszabb utat tennének meg, mint ha a Julinál találkoznának. A jóbarátok közül ki úszott a leglassabban? Találkozásukat illetően melyik a legkedvezőbb hely (vagyis mikor gyalogolnak a legkevesebbet)? Rajzold meg mindegyik gyerek útvonalát.
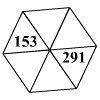
Az ábra üresen hagyott háromszögeibe
írjatok egész számokat úgy, hogy minden három háromszög által
alkotott trapézban valamely két szám összege a harmadik számmal
legyen egyenlő.
Mónika az ábrán látható
számegyenesen választott egy számot. Azután kijelölt rajta még
további két számot úgy, hogy az egyik ötszöröse a választott
számnak, a másik 5-tel nagyobb a választott számnál. Így az A, B
és C pontokat kapta, melyek kölcsönös távolságaira érvényes:
|AB| = 8 cm és |BC| = 6 cm. A számegyenes mely számát
választotta Mónika?
![]()