Gyors herceg meghívta Lassú hercegnőt a várába. Sokáig nem jött, ezért elébe ment. Két napi vándorlás után a hercegnő útjának egy ötöd részén találkozott vele. Együttesen már a hercegnő sebességének kétszeresével haladtak tovább. A herceg várába a találkozótól számítva a második szombaton érkeztek. Melyik napon találkoztak, ha várából a hercegnő pénteken indult el?

A 4 cm oldalhosszúságú négyzet belsejében 1 cm átmérőjű kör úgy mozog, hogy állandóan érinti a négyzet belsejét. Számítsátok ki a területét a négyzet azon részének, amelyet a mozgó kör soha sem takar le.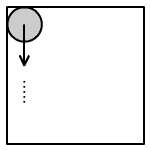

Péter, Mojmír, Károly és Éva a kerületi versenyen tovább jutottak. Utána az iskolában a következő képpen nyilatkoztak:
   Éva: „Négyünk közül nem voltam se első, se utolsó.“
   Mojmír: „Négyünk közül nem voltam utolsó.“
   Károly: „Négyünk közül én voltam az első.“
   Péter: „Négyünk közül én voltam az utolsó.“
Tudjuk, hogy három gyermek igazat mondott és egy hazudott. Ki volt közülük a legjobb a kerületi versenyen?

A felhőkarcoló takarítónője a lépcsőket mosta. Hogy munkája jobban teljen, számolgatta a megmosott lépcsőket. Az összes lépcső pontosan felének felmosása után szünetet tartott. Rövid szünet után újból munkához látott és tovább folytatta a lépcsők számolgatását. A megmosott lépcsők számára való visszaemlékezésénél megtévedett. A helyes három számjegyű számot hátulról „olvasva“ kisebb számot kapott. Ebből a kisebb számból kiindulva számolgatta tovább a lépcsőket. A lépcsők felmosása után 746-os számhoz jutott. Hány lépcsőt moshatott fel a valóságban, ha már többször nem tévedett meg?