Pitagorasz verseny,  5. évf.,  1986/87,  III. ford. feladatai

  1. Az osztályban 31 tanuló van. A kitüntetettek száma 5-tel több mint a fiúk száma. A nem kitüntetettek száma 2-vel kevesebb mint a fiúk száma. Hány lány van az osztályban?

  2. A király az oszlopban álló 3 bölcsnek kalapot tesz a fejére. Minden bölcs az előtte állók kalapját látja, de nem látja a mögötte álló bölcsek kalapjait és saját kalapját sem. A király azt mondta nekik: Mindegyikteknek a fején vagy fehér, vagy fekete kalap van. Volt két fehér és három fekete kalapom. Állapítsátok meg, hogy milyen színű kalap van a fejeteken.
    Az utolsó az oszlopban egy idő után így szólt: "Az én fejemen fekete kalap van."
    Milyen kalap volt a másik két bölcs fején?

  3. Egy kétjegyű szám számjegyeinek összege 10 és osztható 13-mal. Melyik ez a szám?

  4. Írjátok fel azt a legkisebb háromjegyű számot, amely páratlan és a számjegyeinek összegével osztható maradék nélkül.

  5. Oldjátok meg az egyenletet:
    3 . x  -  5  =  22

  6. Keressétek meg az összes olyan természetes számot, melyre érvényes:
    1024 . x  +  5  <  10000

  7. Hasonlítsátok össze nagyság szerint és írjátok fel a legkisebbtől a legnagyobbig:

  8. Számítsátok ki az ábrán levő alakzat területét:

  9. Számítsátok ki:
    66 . 666  +  34 . 6  +  34 . 60  +  34 . 600

  10. Kerekítsétek ki egy tizedes helyre:
    0,1 . ( 153,2  -  14,1  +  0,023 . 0,0172 )

  11. Az x változó helyére helyettesítsétek be a 2,72-t és számítsátok ki:
    3,1 . x  -  0,6  +  1,9

  12. Jancsi betévedt az elvarázsolt erdőbe. Minden nap a sárkányokkal küzdött. Az első sárkánynak 4 feje volt, a másodiknak 7 feje, a harmadiknak 10 feje, és így tovább. Jancsi összesen 91 sárkányfejet vágott le. Hány sárkányt ölt meg?

  13. Az ABC egyenlő oldalú háromszög oldala 3 cm. A háromszög oldalain felvett pontok (lásd az ábrát) az oldalakat három egyenlő részre osztják fel. Hasonlítsátok össze az XT, YZ, WZ, ZT szakaszok hosszát és írjátok le a legrövidebbtől a leghosszabbig!

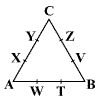
  14. Helyettesítsétek a betűket számjegyekkel (ugyanazon betűk ugyanazon számjegyet jelentik, külömböző betűk külömböző számjegyet jelentenek).
    AA  +  BB  +  CC  +  ABC  +  ABC  =  DDE

  15. Az ABC egyenlő szárú háromszögre, melynek alapja AB érvényes:
    a BC szár hossza egyenlő a BC oldalhoz tartozó magasság hosszával.
    Határozzátok meg a CAB szög nagyságát.