Mekkora szöget ír le 3 óra alatt az óra nagymutatója?

Hány percből áll 7 nap?

Számítsátok ki az ABCD négyzetben a belső szögek összegét!

Írjátok le a legkisebb eredményt jelző betűt:
A = 5,6 . 7,2 . 5,7
B = (0,4 + 0,74) . 0,104
C = 55,55 : 66,66
D = (10,57 – 3,25) . (10,56 – 5,24) . (27,48 – 27,480)

Hány olyan egyjegyű szám van, amellyel az 50 maradék nélkül osztható?

Hány számjegyet kell leírnom, ha meg akarom számozni egy 20 lapból álló füzet minden oldalát? (a borítót nem számozom)

Milyen számot kell az x helyére írni az egyenletben:
5,25 + 2 . x = 15,25

A táblázatban számok vannak. Írjátok le azt a számot, amelyik hiányzik!

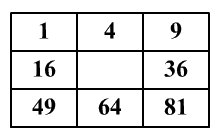
Az állatkertben három leopárd él, életkoruk összege 27 év. Hány évesek lesznek összesen 5 év múlva?

Az összeadás eredményét írjátok le kilogrammokban:
0,5 t + 30 000 dag + 5 q + 20 000 g =

Gyurinak egy kockát kellett összeraknia 2 cm élű kis kockákból. A kocka alapját 81 kis kockának kellett képeznie. Hány kis kockára volt szüksége az egész kocka megépítéséhez?

Bálint ez iskolába három különböző utcán tud eljutni. Az iskolából haza mindig másik utcán megy, mint amelyiken az iskolába ment. Hány nap tud úgy eljutni az iskolába és onnan haza, hogy mindennap különböző utat tegyen meg?

Hány páratlan kétjegyű szám van?

Milyen számot kell a 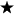   helyére írni a példában, hogy az eredmény a legnagyobb háromjegyű szám legyen?
3568 – ( 3568 – ) =

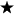A diákok sorban álltak az ebédért. Kinga elölről a tizenhatodik, hátulról a huszonnegyedik volt. Hány diák állt az ebédért?