Egy sorba 16 fát ültettek. Két szomszédos fa között a távolság 4 méter volt (mindenhol egyforma). Hány méter távolságra van az első fa a fasor közepétől?

Keressétek meg a 24 összes osztóját! Alkossátok meg ezeknek a számoknak a reciprokát és ezeket adjátok össze! Írjátok le az eredményt tizedestört alakjában!

Írjátok le, hogy hány olyan száznál nagyobb, de ezernél kisebb páros természetes szám van, amelyet elölről és hátulról is ugyanúgy kell leírni!

A raktárban a könyvek árát 20%-kal kell csökkenteni. Milyen tizedestörttel kell a raktárosnőnek beszoroznia az eredeti árat ahhoz, hogy meghatározza az új árat?

Egy ismeretlen szám egy nyolcada 3. Írjátok le, hogy mennyivel egyenlő az ismeretlen szám egy harmada!

Csongor összeadott öt egymást követő természetes számot, amelyek közül a középső s volt. Írjátok le ezeknek a számoknak az összegét egyszerűsített formában!

Az egérke talált egy hasáb alakú sajtot és elkezdte rágcsálni. Mindennap ugyanakkora mennyiséget harapott belőle. 28 nap múlva egy olyan hasáb alakú sajtja maradt, amelynek méretei az eredeti hasáb méreteinek a fele voltak. Hány napig tart ki még az egérkének ez a sajtdarab?

A kocka lapjának a területe 50 cm². Számítsd ki a kocka felszínét négyzetcentiméterekben!

Számítsátok ki:

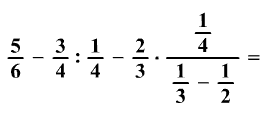
Az eredményt írjátok le törzsalakú tört alakjában!

Írjátok le azt a legnagyobb  d  természetes számot, amelyre a 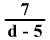tört negatív!

Írjátok le, hogy mennyi a négy harmad egy harmada plussz az egy harmad két harmada! Az eredményt törzsalakú tört alakjában írjátok le!

Írjátok le azt a számot, amely 25 ezrest, 25 százast és 25 egyest tartalmaz!

A zsákban 120 golyó van, három különböző színben. Legkevesebb hány golyót kell a zsákból kivennünk, hogy legalább 3 egyforma színű golyónk legyen, ha mindhárom színből ugyanannyi golyónk van?

Hány háromszög van az ábrán:

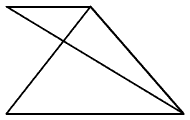
Írjátok le a feladat eredményét:
1,11 – { 1,1 – [ 0,11 – ( 1,11 – 1 ) ] } =