A kisasztal ára 50%-kal emelkedett, majd 50%-kal csökkent. Az eredeti ár hányad részébe kerül most?

Milyen számjegyre végződik a 2²⁰⁰⁴ szám?

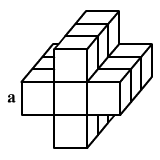
Határozd meg az ábrán látható test felszínét, ha  a = 1 cm.

Írd fel a 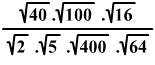   törtet tizedestört alakban!

Oldd meg az alábbi egyenletet:

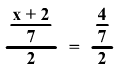
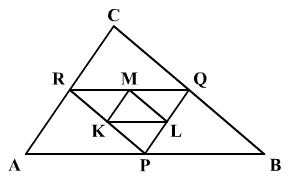
Számítsd ki a KLM háromszög kerületét, ha  a = 10 cm,  b = 8 cm,  c = 16 cm,  és a  P, Q, R, K, L, M  pontok az oldalak középpontjai!

Számítsd ki az összeget:  

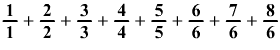
Írd fel melyik szám a nagyobb:
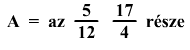   vagy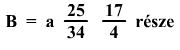  

Számítsd ki:   12,5 : 0,25 : 0,2 : 0,5 : 0,2 =

Hányféleképpen rakhatunk egymás mellé három különböző színű kockát?

Írjatok az A és B helyére számjegyeket úgy, hogy érvényes legyen az egyenlőség:   3A + AB = 60

Állapítsd meg, hogy a  947 718 621  osztható-e 72-vel!

Egy kétjegyű szám egyes helyiértékén  8-as számjegy áll. Ha felcseréljük a számjegyek sorrendjét, az eredeti számnál  45-tel nagyobb számot kapunk. Melyik az eredeti szám?

Írd fel az összes olyan természetes szám összegét, amelyre érvényes:

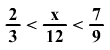
Gondoltam két egész számra. Ha összeszorzom őket  –12-t kapok. Ha összeadom őket  1-et kapok. Melyik számokra gondoltam?