A  Δ  helyére írj számjegyet úgy, hogy érvényes legyen:   3Δ . 5 = Δ55

Határozd meg, hogy a  9 432  és a  16 622  számok közül melyik osztható 72-vel?

Számítsd ki a 20 összes osztójának összegét!

Hány százalék az  50%  20%-a?

A táborban a gyerekek fele uszodába ment, harmada síelni, a hetede pedig videót nézett a könyvtárban. Egyszerre 41 gyerek ment el. Hány gyerek maradt a szobákban?

67 koronát ötkoronásokkal és kétkoronásokkal fizettünk ki. Legfeljebb hány ötkoronást használhattunk fel?

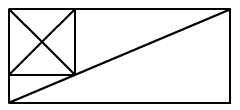
Hány háromszög van az ábrán?

Írd fel azoknak a számjegyeknek a szorzatát, amelyeket a  47Θ56  számban helyettesíthetünk a  Θ  helyére úgy, hogy a szám hárommal osztható legyen!

Határozd meg azt a számot, amely a számegyenesen a  – 0,67  és a  7,24  számok között középen van!

Számítsd ki: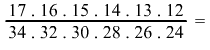  

Az ABC háromszögben érvényes:  α : β = 5 : 7.  A  γ  szög  42°-kal kisebb, mint a  δ.  A  δ  szög az  α  szög külső szöge. Számítsd ki a  β  szöget!

Határozd meg a legkisebb ötjegyű és legnagyobb háromjegyű szám különbségét!

Pitagórus Jancsinak 3 lánytestvére van. Mindhárom lánytestvérnek kettő fiútestvére van. Hány gyerek van a családban?

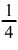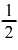Hány százalékkal kell növelnünk az -et ahhoz, hogy -et kapjunk?

Ha felírunk egy kétjegyű számot és összeadjuk a számjegyeit, hány különböző összeget kaphatunk?