-
Az alábbi számok közül
melyik egyenlő a többi négy szorzatával?
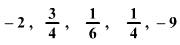
-
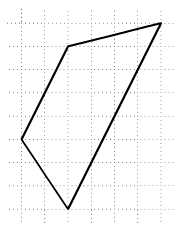
Hány kis négyzetet
tartalmaz az ábrán látható trapéz, melynek csúcspontjai a négyzetháló
rácspontjaiban vannak?
-
Az üzletben 20%-os árleszállítás
van a fürdőruhák minden méretére. Az eredeti árak méretenként
a következők voltak: M1 - 1290 Sk, M2 - 1490 Sk,
M3 - 2190 Sk. Melyik méretű fürdőruha lesz az árleszállítás
után a legolcsóbb?
-
Melyik prímszámokra érvényes?
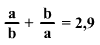
-
Mi a több: egyketted kétharmada
vagy az egyharmad háromnegyede?
-
Az öttagú számhalmazból
írd ki azokat a számokat, melyek maradék nélkül oszthatók 4-gyel
és 9-cel:
{ 1 524 348, 5 124 348,
5 123 484, 5 443 182, 4 235 418 }
-
Az ábrán Ádám és Éva látható.
Valóságban Ádám 182 cm magas. Hány cm magas Éva?

-
Melyik szám nagyobb:
63-nak az 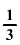 -a
vagy a (33)2-nak az
-a
vagy a (33)2-nak az 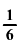 -a?
-a?
-
Számítsd ki a derékszögű
háromszög területét, ha átfogója 50 cm és az egyik befogója
30 cm hosszú.
-
Ha az ismeretlen számot
megszorozzuk 7-tel, vagy ha növeljük 7-tel, mindig egyforma eredményt
kapunk. Határozd meg az ismeretlen számot.
-
Oldd meg az egyenletet az R
számok halmazán:
– { – [ – ( – x + 2 ) – 3 ] + 5 } – 7 + x =
0
-
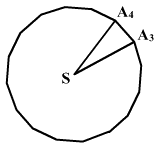
Az A1, A2,
..., A16 pontok egy szabályos 16-szögnek a csúcsai.
Határozd meg az A3SA4 szög nagyságát.
-
A Misi bizonyítványában
levő jegyek összege 23. 2-vel több egyese volt mint kettese és kétszer
annyi mint hármasa. Másfajta jegyei nem voltak. Hány tantárgyból
voltak jegyei Misinek a bizonyítványban?
-
Hány háromjegyű számot
tudsz alkotni a 0, 2, 4, 6 számjegyekből úgy, hogy az
egyik számjegy se ismétlődjön, és a számok nagyobbak legyenek
300-nál?
-
A sütemények formával való
kiszaggatása után a maradék tésztát újra felhasználják. 3 sütemény
kiszaggatása után a maradék tészta egy süteményre elég.
Legfeljebb hány süteményt lehet kiszaggatni a tésztából, ha elsőre
324 süteményt szaggattunk ki?
