-
Pótold számjeggyel a
csillagok helyét, ha tudod, hogy a csillagok alatt egyforma számjegyek
vannak:
268,17 .  ,8 = 1
,8 = 1 55,386
55,386
-
Számítsd ki: 8
. 2/5 + 4 . 4/10 + 30 . 8/20 – 12 . 16/40
-
Hány háromszög van az ábrám?
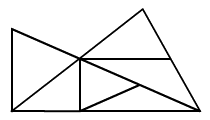
-
Hány liter folyadék fér a
téglatest alakú edénybe, ha az edény méretei: 2,5 m ;
3 dm ; 6,2 m ?
-
A háromszög egyik belső szöge
háromszor kisebb mint a másik és négyszer kisebb mint a harmadik
belső szög. Mekkora a második belső szög?
-
A turista 1/3 óra alatt a
tervezett útja 2/5-ét tette meg. A következő 1/6 óra alatt 1,04
km-t tett meg. Hány kilométert tervezett megtenni a turista, ha tudjátok,
hogy mindig állandó sebességgel haladt.
-
A következő betűk közül
melyek középpontosan tükrösek?
H , E , Z , M , N , O
-
Misi egy edényben levő
folyadékhoz még hozzáöntötte az edényben levő folyadék mennyiségének
5%-át. Hány liter folyadék volt eredetileg az edényben, ha a hozzáöntés
után a folyadék mennyisége 12,6 liter volt.
-
Határozd meg a 210 ,
315 és a 30 legnagyobb közös osztóját.
-
Számítsd ki: 346
– ( 20 – 114 – ( 25 – 78 – ( 42 + 18 ) ) )
-
Hány kilogrammal kisebb a 36
tonna 2/6-a mint a 45 tonna 27%-a?
-
Határozd meg az y értékét,
ha tudod, hogy csak egész szám lehet:
37,2 < 4,8 y – 11 < 40,8
-
A moziban 16 sor, soronként
42 szék van. Hány koronát fizettek a nézők a belépőkért összesen,
ha minden sor foglalt volt, és az első 8 sor jegyeiért 32 koronát,
a többiért 36 koronát fizettek?
-
Hány olyan háromjegyű szám
van, melynek számjegyei prímszámok?
-
Petra kosarában 3 darab 20
koronás és 5 darab 16 koronás csokoládé volt. Számítsd ki a
csokoládék árának aritmetikai átlagát!
