-
Számítsd ki:
0,05 - ( 0,5 - ( 5 - 50 )
) =
-
Hány olyan háromjegyű
szám van, mely osztható 9-cel és a számjegyek összege 12 ?
-
Hány cm a paralelogramma kerülete,
ha oldalai 15,8 mm és 18,5 dm ?
-
Mely számok vannak a számegyenesen
a -10,3 számtól olyan távolságra, mint a
12 és a -1,5 távolsága?
-
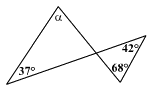
Számítsd ki az α
szög nagyságát!
-
Anni egy negyed kenyérért
4,80 Sk-t fizetett. Mennyit fizet Janka egy harmad ugyanilyen kenyérért?
-
Írd le az eredményt tizedes
számmal:
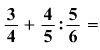
-
Milyen számjegyek vannak a
hiányzó helyeken?

-
Bontsd fel az 1638-at prímszámok
szorzatára!
-
Old meg az egyenletet:
x : 1,8 = 567 - 29
-
Hány különböző téglalap
létezik, melynek kerülete 54 cm és oldalai egész számok
(cm-ben)?
-
Keress egy megoldást
az x . x + 15 . x =
126 egyenletre!
-
Színezd ki a rajz egy négyzetét
úgy, hogy az alakzat tengelyesen szimmetrikus legyen!

-
Jancsinak 546 koronája van.
Péternek háromszor több koronája van, mint Jancsinak, de 30 koronával
kevesebb, mint Palinak. Hány koronája van Palinak?
-
Melyek azok a törtek, melyek
nagyobbak mint 2, de kisebbek mint 3,5 és a nevezőjük 3 ?
