-
Pótold a hiányzó számjegyeket a következő
rendszeresség betartásával:
11 , 12 , 15 , 20 , 27 , 36 , 47 , ... , ... , ... , ...
-
Old meg az egyenletet:
5 . a . 3 = 105
-
A csillag helyét pótoljátok olyan számjeggyel,
hogy ha a kapott számot elosztjátok 9-cel a maradék három legyen:
2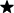 6
6
-
Írjatok fel minden olyan háromjegyű számot,
amelyek számjegyeinek összege 3.
-
Az apa egy év múlva kétszer olyan idős
lesz mint a fia. Ma együtt 58 évesek. Hány éves a fiú?
-
Hány páros szám megoldása ennek az egyenlőtlenségnek?
544 < x < 703
-
Számítsd ki:
5 . 6 . 7 . 8 : 7 : 6 : 5 : 4
-
A moziban 100 ember van. Annyi férfi van
mint nő, de gyerekek 10-zel többen vannak mint a férfiak. Hány
felnőtt van a moziban?
-
Rajzolj két háromszöget úgy, hogy az
egyesítésük (úniójuk) és a metszetük (közös részük) is háromszög
legyen.
-
Számítsd ki:
25 . 23 . 4
-
A csillagok helyét pótold olyan számjegyekkel,
hogy érvényes legyen:
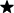 5
5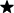 + 7
+ 7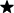 8 =
8 =
 303
303
-
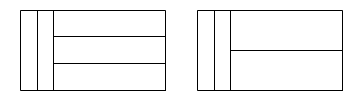
Mennyivel több téglalap van az első képen
mint a másodikon?
-
Oszd szét a számokat három csoportba úgy,
hogy mindhárom csoport összege egyenlő legyen:
3 , 4 , 7 , 9 , 11 , 12 , 13 , 16
-
Hány olyan kétjegyű szám van, amelyek
nem többszörösei a 13-nak?
-
Egy edényben, amelybe nem látunk bele 4 kék,
5 zöld és 7 fekete golyó van. Milyen legkevesebb mennyiségű
golyót kell kivennünk, hogy biztosak legyünk benne, hogy a
kisszedett golyók közt legalább egy kék és szintén legalább egy
zöld golyó legyen?
